Abstract
Objectives: To investigate the effects of risk factors on recurrence and death in breast cancer patients, taking into account the dependence between recurrence and death as well as the heterogeneity among individuals. The other aim of this study was to make predictions of death risks with a dynamic model that includes patient’s history and different horizons.
Methods: The data of 465 patients who had undergone surgery at the Istanbul University Oncology Institute, Istanbul, Turkey, between 2009 and 2016 were used. For data analysis in this retrospective study, the authors applied the joint frailty model, and the predictions were obtained using dynamic prediction methods that consider the patient’s history. The Brier score was used to evaluate the accuracy of the estimations.
Results: A positive relationship was found between recurrence and death, and heterogeneity was found among patients (p<0.001, p=1.008, p=2.945). The effects of Cerb-B2, tumor type, remaining lymph nodes, neoadjuvant chemotherapy, and surgery type were statistically significant for death and recurrence (p<0.05, relative risk [death, recurrence] = [2.5, 11.86], [2.065, 2.798], [1.852, 3.113], [4.211, 9.366], [1.521,1.991]). The Brier score values used in the evaluation of the predictions obtained by the dynamic prediction methods were found to be below 0.30.
Conclusion: The use of joint frailty models is recommended for the detection of heterogeneity effects and dependence between recurrence and death. Through models in survival analysis, researchers can obtain more accurate parameter estimates. A significant variance of frailty indicates different death risks for the same characteristics.
Cancer is one the most significant health problems. The World Health Organization (WHO) reported breast cancer to be the second-most frequently detected cancer worldwide, and breast cancer is the most frequently detected cancer type in women. Previous studies have reported that breast cancer made up 11.6% of patient cancer diagnoses in 2018.1,2 With the rise in the number of patients diagnosed with breast cancer throughout the world, studies in this field have reported significant advances, and new drugs or treatment methods are being developed each year. At this stage, researchers use survival analyses in the investigation of the efficacy of treatments and the risk factors affecting the disease. In most studies, recurrence and death are evaluated separately.3 However, it does not seem reasonable to consider these 2 events as being independent of each other. Generally, recurrence and death are correlated with each other. In addition, the possibility of experiencing related events is higher in some individuals than in others. These differences, namely, heterogeneities, among individuals are associated with genetic structure, the effects of environmental factors, nutritional habits, and various other factors. Ignoring these heterogeneities among individuals will lead to biased results. In recent years, researchers have proposed joint frailty models that consider these heterogeneities and the dependency between recurrence and death as overcoming this disadvantage.3,4
The present study aimed to investigate the association between recurrence and death in breast cancer patients and to investigate the effects of risk factors on death and recurrence using joint frailty models. The risk of death was estimated using the dynamic estimation method that considers the patient’s history of the event. The predicted accuracy was evaluated by the Brier score.
Breast cancer and risk factors
Breast cancer, as a metastatic type of cancer, has a higher survival rate and better prognosis with screenings for early diagnosis. However, treatment is highly difficult in the advanced stages. Breast cancer patients require follow-ups after the administration of treatment.5,6
While risk factor evaluation for breast cancer shows that it rarely develops before the age of 30, the risk increases with advancing age and in a gradual manner after menopause. In addition, genetic factors are also important, as patients with a family history of breast cancer have a higher risk of developing the disease. The risk of the development of breast cancer is also higher in patients diagnosed with colon, ovarian, and uterine cancers. Hormones play a significant role in the development of breast cancer. In addition to these factors, there are factors that can be controlled by the individual, such as smoking, alcohol consumption, lack of physical activity, and being overweight, all of which increase breast cancer risk. However, these factors may be eliminated by taking personal precautions.7,8
In recent years, there have been a great number of developments in breast cancer treatment. However, the clinical condition and disease process for each patient varies, showing that the disease is heterogeneous. Therefore, recent developments in the personalized treatments for the disease are proving useful.9
Prognostic factors are also important for the development of individualized treatments. Individual factors such as the clinical stage of the disease, treatment type, tumor number and size, hormone receptors, and the number of remaining lymph nodes have a high impact on the mortality rate.10
Joint frailty models
In cancer studies, there are generally several endpoints before death. All these different endpoints must be simultaneously evaluated in order to increase the efficacy of the clinical decision procedure. Because most breast cancer deaths are related to recurrence, patients with recurrence are expected to have a higher risk of death than patients without recurrence. Thus, patients experiencing recurrence are frailer than others. Moreover, this heterogeneity (frailty) results from differences in recurrence as well as unobserved factor effects. Frequently, there are heterogeneities among patients because of unexplained factors. As it is not possible to measure all factor effects in models, in these situations, joint frailty models should be used. These models simultaneously investigate the recurrence and death processes and consider the dependency between recurrence and death. Both events are randomly associated during the investigation. Because unobservable effects cause heterogeneity, the random effects of the source of this heterogeneity are taken into consideration within the model. The frailty term νi is regarded as independent and considers the heterogeneity associated with the explanatory variable that cannot be observed, the mean being “1” and the variance “θ.” The variance of the random effect is the measure of the heterogeneity among individuals. In addition, the frailty term may differ for the 2 events (recurrence and death).11,12
The researcher used the following models to obtain the risk functions for recurrence and death in time (t):
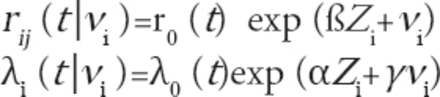
Here, i is the index individual, j is the recurrent event, Zi is the observed explanatory variable vector of the individual, which is the same for death and recurrence events in the models above, β is the regression coefficient for recurrence, and α is the regression coefficient for death. The γ is the value which demonstrates the association between recurrence and death. Higher γ values indicate a higher association between recurrence and death. The γ coefficient can be interpreted when the θ value is statistically different from zero, namely, when the heterogeneity is statistically significant in the data set.13 The parameter estimates in the model were obtained with the maximization of the penalized log likelihood. The penalized log likelihood was expressed as below for the joint frailty models.11
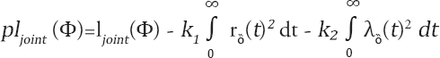
Here, k1 and k2 are the positive smoothing parameters. The smoothing parameter for recurrence (k1) was obtained using the shared frailty model, and the smoothing parameter for death (k2) was obtained using Cox regression.
Dynamic prediction
The calculation of death risks is important for choosing the appropriate treatment options for the patient and for making individualized treatment decisions. In addition, it is important to estimate the risk of death for a patient using advances in personalized medicine. For this purpose, dynamic prediction provides many advantages in the estimation of the risk of death, as it considers the entire event history of the patient, and the dynamic prediction can be updated when a new event occurs. Calculations are not only instantaneous for prediction t, but also for time intervals (horizons) using patient’s history. There are 3 different estimation methods for dynamic prediction. The first estimation calculates the risk by taking into account the exact j recurrences before prediction t. In the second estimation, a recurrence of at least j in the patient’s history before the prediction t is taken into account, whereas the jth events occurring between recurrence and prediction time are not considered. In the last estimate, the recurrence history of a patient is considered during calculations. Only the parameters obtained from the joint frailty model are used for the estimation of death risk. In other words, the recurrence history is taken into account indirectly with the parameter estimates.
The estimation t is expressed by t and the estimation window is expressed by w. The dynamic models are concerned with the estimations between t and w (horizon time). i is the death time of i. patient, Xij is the jth recurrence number of i. patient, ZijR is the related covariates with recurrence and ZiD is the related covariates with death. The equations SijR (t) = P(Xij≥t) and SiD (t) = P(Di≥t) express the survival functions of recurrence and death, respectively. The term ξ=(λ0R (.),λ0D(.),β, α, θ) includes all the parameters of the patient. For the predictions, the risk of death should be defined based on the patient’s history of recurrence. There are 2 different recurrence histories for this: the completed recurrence history Hji,1 (t) and partial recurrence history Hji2 (t).14
After obtaining the predictions, the Brier score, used for the accuracy of the estimates, is calculated by the mean squared error of the probability forecasts. The Brier score value is between 0 and 1. The closer the score is to 0, the greater the accuracy of the risk estimates.15
Methods
Four hundred and sixty-five patients who had undergone surgery at the Oncology Institute, Faculty of Medicine, Istanbul University, Istanbul, Turkey between 2009 and 2016 were included in the study. The study is a retrospective study. All procedures performed were in accordance with the ethical standard for studies involving human participants of the institutional or national research committee and the 1964 Helsinki Declaration and its later amendments or comparable ethical standards. Permissions were obtained from the Istanbul University Oncology Institute (30/03/2018-105420). The patients had no previous history of other cancer types. The patients were followed up for periods ranging to 10 years following their surgery date. Patients made routine visits to the hospital.
The inclusion criteria for the patients were an accurate diagnosis of breast cancer and a follow-up of at least 2 months after surgery. Observations missing definitive variable data were excluded from the study. The clinical stages of the patients in the study consisted of stage 1, 2 and 3 cancers. Patients with stage 4 were excluded from the study. Time to event was defined as the time between the surgery date and the date of each recurrent event or death. There are no missing data in our study. The investigated factors included age (≤40, >40), Cerb-B2 (human epidermal growth factor receptor 2 [HER-2/neu] [positive, negative], tumor type [invasive ductal carcinoma [IDC], others]), number of lymph nodes remaining after surgery (≤5, >5), neoadjuvant chemotherapy [NACT] (no, yes), clinical stage (Stage 1, Stages 2A-2B, Stages 3A-3B), Ki-67 (≤25%, >25%), surgery type (breast conserving surgery [BCS], modified radical mastectomy [MRM]), and hormone receptor (estrogen receptor [ER] or progesterone receptor [PR] [positive, negative]). Ki67 and age cut-off points were taken in accordance with the studies in the literature.16,17
Statistical analysis
The factor effects were evaluated via a joint frailty model that considers the dependence between recurrence and death as well as the heterogeneity among patients. In the model, parameter estimations were obtained by penalized likelihood method. The smoothing parameters were obtained via a shared frailty model and the Cox model. Parameter estimations were obtained by a robust Marquardt algorithm consisting of combinations of the Newton Raphson algorithm and steepest descent algorithm. The model fit was analyzed by evaluating the Martingale residues. The risk of death was estimated by dynamic estimation method and predicted successes were evaluated with the Brier score. The analyses in the study were performed using the R.3.5.3 frailtypack package.18
Results
Results were obtained from 465 women diagnosed with breast cancer. The follow-up period varied between 2 and 127 months. The patients who developed no recurrence constituted the majority of the study population (n=361; 77.6%), while 83 of the patients in the study experienced only one recurrence and 21 had 2 recurrences. In terms of deaths, a total of 155 deaths were observed (33.3%). The descriptive statistics of the data are presented in Table 1. According to the data, 24.3% of the patients were under the age of 40, and 21.7% had positive Cerb-B2 values. When we considered the number of lymph nodes after surgery, we found fewer than 5 in 74.4% of the patients. The tumor type was IDC in 82.8% of the patients and 50.8% of the patients underwent BCS surgery and 49.2% MRM. We evaluated the stage in 2 categories. In our data, chemotherapy treatment was applied after surgery to 64.3% of the patients. It was observed that 71.6% of the patients were positive for the ER or PR receptor (Table 1).
Descriptive of patients.
In order to decide the smoothing parameters before performing the joint frailty model, we used the shared frailty model for recurrence and the Cox model for death. The Kappa 1 and 2 values were obtained as 120,000 and 85,000 at the end of the model. The results for the joint frailty models in Table 2 were obtained after the use of smoothing parameters. In Table 2, θ characterizes the dependence between the recurrence process and death with a frailty. A positive relationship was found between the recurrence and the death process. This meant that a higher recurrence event caused a high risk of death. The number of previous recurrences affected the risk of death, given the frailty (random effect). Furthermore, in our data, the patients were heterogeneous. The heterogeneity among patients was statistically significant (p<0.001, p=1.008, p=2.945) (Table 2).
Joint frailty model results
When considering the factor effects, we saw that Cerb-B2 (p=0.026), tumor type (p=0.004), number of lymph nodes after surgery (p=0.008), NACT (p<0.001), clinical stage (p=0.050), surgery type (p=0.050) and hormone receptor (p<0.001) had significant effects on recurrence risk. However, the age group and Ki-67 had no statistical effect on recurrence (p>0.05). Positive Cerb-B2 had a higher risk of recurrence (relative risk [RR] = 2.500). Other tumor types had a higher recurrence than IDC (RR = 2.065). The RR of patients having more than 5 lymph nodes after surgery was 1.852-fold higher than that of patients having fewer than 5 lymph nodes. The RR of patients who received no chemotherapy was 4.211-fold higher than those patients who received chemotherapy. Therefore, receiving postoperative chemotherapy was highly effective on the RR of the patients. The evaluation of the recurrence results for the clinical stage showed that the RR of patients in clinical stage 3 was 1.889-fold higher compared to that of patients with clinical stages 1 or 2. The RR for the patients who had MRM surgery was 1.521-fold higher than that of patients who underwent BCS surgery. Patients who did not had neoadjuvant chemotherapy had more recurrence and death risk than those who underwent neoadjuvant chemotherapy. Patients with hormone receptor negatively had less risk of recurrence than those who were positive (RR = 0.460) (Table 2).
The evaluation of the joint frailty model for death showed that age group, clinical stage, and hormone receptors were found statistically not significant for death risk (p>0.05). However, the variables Cerb-B2 (p<0.001), tumor type (p=0.017), number of lymph nodes after surgery (p=0.007), NACT (p<0.001), Ki-67 (p=0.046) and surgery type were found to be statistically significant for death risk.
The death risk of patients with Cerb-B2 positivity was 11.860-fold higher compared to those with Cerb-B2 negativity. The effect of Cerb-B2 positivity on death risk was found to be significantly higher. The death risk of patients having more than 5 lymph nodes after surgery was 3.113-fold higher than the death risk of patients with fewer than 5 lymph nodes (Table 2).
The IDC tumor type was identified as having an increasing effect on death risk (RR = 2.798). The death risk of patients who received no chemotherapy after surgery was 9.366-fold higher than that of patients who received chemotherapy. The RR for patients with surgery type MRM was 1.991-fold higher than that of patients who underwent BCS surgery. Patients with higher Ki-67 had higher death risk (RR = 2.029) (Table 2). Therefore, Cerb-B2, tumor type, number of lymph nodes after surgery, NACT and surgery type were found to have effects both on recurrence and death risk.
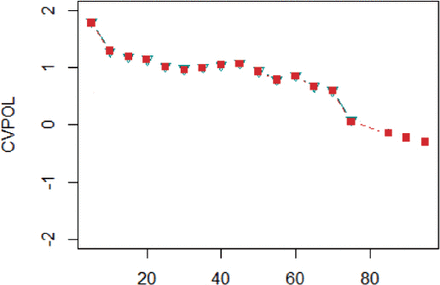
In Figure 1, the cross-validated prognosis observed loss (CVPOL) results were shown for the predictions. We can say that the power of the forecast increases as time progresses.
Cross-validated prognosis observed loss.
The death risk of patients was estimated in the next stage. To estimate the risk of death, we used the dynamic estimation method, which evaluates the historical information of recurrence and death updated with new events. The death risk was calculated for all patients using dynamic prediction, and, according to the estimations, 3 different death risks were obtained. We cannot show the risks of patients due to the large amount of space required. The Brier score values were calculated to test the accuracy of the death risks obtained using the 3 different estimation methods. Death risks were calculated for 3 different prediction times, and the Brier scores were used to determine any differences between the prediction times.
Tables 3-5 show the Brier score values for checking the accuracy of the death risks obtained via the dynamic estimation methods using the estimated t = 30, t = 40, and t = 50 taken with different horizons. According to the Brier score, the values of estimation 3 were higher than those of estimations 1 and 2. Therefore, the accuracy of the results of estimation methods 1 and 2 was higher than that of estimation 3. The reason for this was that the estimation 3 method predicted the risk of death based on parameter estimates only, without considering the recurrence histories. The Brier score values of the estimations did not exceed 0.30 and were close to 0. This shows the accuracy of the estimations using the joint frailty model (Tables 3-5).
Brier scores for the prediction time t=30 and for different horizons.
Brier scores for the prediction time t=40 and for different horizons.
Brier scores for the prediction time t=50 and for different horizons.
Discussion
The study aimed to describe the joint frailty models and to evaluate the possible risk factors by accounting for the association between recurrence and death in breast cancer. We used the joint frailty models in the evaluation of recurrence and death in the study. The variables that might be effective for 2 different survival endpoints were simultaneously estimated with the help of the model. The model provided the estimates of the parameters using all the data of patients as well as the relationships between events. Joint frailty models eliminate biased results by considering the dependencies between recurrence and death and the heterogeneities among individuals. Another advantage of the method is that the effects of different covariants may be investigated for 2 different events. These covariants may vary by following the time or may be independent of the time.
The results of our study showed that there was a positive association between recurrence and death. Death risk was affected by the development of recurrence. This finding supports the results of various studies. O’Shaughnessy19 observed a significant association between metastatic events and death. Similarly, Elkhuizen et al20 in their study, found a significant association between regional recurrences and death. Osmani et al21,22 also evaluated the dependencies between local and metastasis recurrence with breast cancer patients in their study conducted in Iran.
In their study, Mauguen et al14 stated that, in cancer study, generally, one or more events occurred before the death event and that accuracy of clinical decisions could be increased when all of these events in the patient’s history were taken into consideration in the estimation of the risk of death. The probabilities of death between the estimated t and the horizon t were determined using the dynamic estimation method with data from 1161 patients with operative breast cancer between 1989 and 1993. The researchers took age, tumor volume, HER2+, hormone receptor, nodal involvement, histopathological stage, and peritumoral vascular invasion as factors in the study. The frailty effect was obtained as 1.04. Similar to our study, a positive correlation was found between the risk of recurrence and death. The effect of the frailty term on death risk was found to be great. The effect of tumor size on both death and recurrence was statistically significant. As for the age group, we found that the risk of death for individuals aged 55 years and older was higher than for those aged 40-55 years, while the risk of recurrence was found to be lower than those aged 40. In our study, no significant relationship was found between age and recurrence and death risks. Mauguen et al14 found that the hormone receptor variable had a statistically significant effect on recurrence risk. We think that these findings that differ from our study could have resulted from using different variables in the models. Similar to our study, when the dynamic estimation results were evaluated, Mauguen et al14 found that the estimations obtained from the first and second estimation methods were close to each other and that the estimation error was great with the third estimation method.
Osmani et al21 investigated the relationship between local recurrence and metastasis using data from 342 breast cancer patients. They did not use the relationships between death and recurrence but examined only the relationships between 2 recurrent events using joint frailty models. As a result, they observed that patients had different risks even though they had the same variable characteristics.
In their 2018 study, Osmani et al22 used the retrospective data of 342 patients with breast cancer to examine the relationship between recurrence and death using joint frailty models. They included lymph node status, age, hormone receptor status, tumor size, HER2+, and grade factors in the model. They found that age had no significant effect on recurrence and death risks (40 years and under compared with other age groups) and that there was no significant relationship between local recurrence and death.
Gohari et al23 found the variance of frailty as 0.31; however, Rondeau et al11 determined it to be 0.35. We found the frailty variance as 0.999 in our study. This showed that heterogeneity was higher among the breast cancer patients in our study. There were differences for recurrence and death risks for individuals with the same descriptive features. There was an association among the patients which showed that the model was appropriate for the data.11,21-23
In our study, the frailty term was assumed not to have changed over time in the estimations. However, the effects of the unobservable factors might have changed over time, and, in such an event, the frailty term might also have changed over time. However, in our study, the estimates were performed assuming that the frailty term was stable during the follow-up.
Study limitations
To illustrate the advantages of joint frailty models, a simulation study can be performed. Due to the small rate of recurrence and small percent of death, the Brier score should be interpreted with caution.
In conclusion, we can say that recurrence events are generally associated with death in oncology studies and that there is heterogeneity among individuals. The use of joint frailty models rather than the classical statistical methods in such cases would decrease the bias. The use of joint frailty models is recommended for the detection of heterogeneity effects and for the detection of the dependence between recurrence and death. Using these models in survival analysis may result in more accurate parameter estimates. A significant variance of frailty indicates different death risks for the same characteristics. The dynamic predictions can be used for the best treatment choices in the personalized medicine field.
Footnotes
Disclosure. Authors have no conflict of interests, and the work was not supported or funded by any drug company.
- Received January 15, 2020.
- Accepted April 6, 2020.
- Copyright: © Saudi Medical Journal
This is an open-access article distributed under the terms of the Creative Commons Attribution-Noncommercial-Share Alike 3.0 Unported, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.